机器学习与R语言实战笔记（第三章）

2021年11月28日 写评论

 R和统计，R语言和统计是一对兄弟，相互难以离开呀！

这里记录下这本书里我之前不了解的内容，欢迎一起交流！向量的模式作者写了个函数来干这件事，我学习下，登上巨人的肩膀。我的理解，这个是相当于motif，计数最多的元素的意思。

mode <- function(x) {
  temp <- table(x)
  names(temp)[temp == max(temp)]
}

3.5 在R中进行多元相关分析

为避免单个变量的负面影响，以下是相关矩阵和协方差示进行多元相关分析的过程：

# 多元线性相关
data("mtcars")
# 协方差矩阵(线性相关度)
cov(mtcars[1:3])
# mpg        cyl       disp
# mpg    36.324103  -9.172379  -633.0972
# cyl    -9.172379   3.189516   199.6603
# disp -633.097208 199.660282 15360.7998
# 相关矩阵（相关程度的大小）
cor(mtcars[1:3])

# mpg        cyl       disp
# mpg   1.0000000 -0.8521620 -0.8475514
# cyl  -0.8521620  1.0000000  0.9020329
# disp -0.8475514  0.9020329  1.0000000
# 相关矩阵热力图
library(reshape2)
library(ggplot2)
qplot(x=Var1, y=Var2, data=melt(cor(mtcars[1:3])), fill=value, geom='tile')

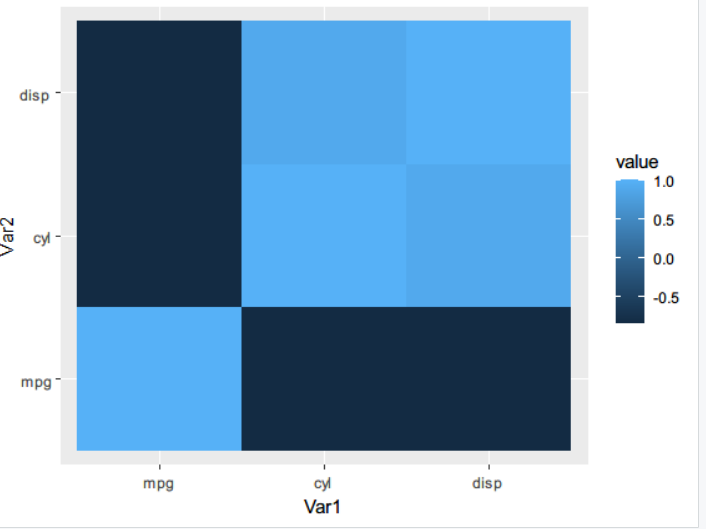
3.6 进行多元回归分析

评估独立及非独立变量间的关联性

# 回归
lmfit <- lm(mtcars$mpg ~ mtcars$cyl)
lmfit
# Call:
#   lm(formula = mtcars$mpg ~ mtcars$cyl)
# 
# Coefficients:
#   (Intercept)   mtcars$cyl  
# 37.885       -2.876 
summary(lmfit) #信息更详细？
# Call:
#   lm(formula = mtcars$mpg ~ mtcars$cyl)
# 
# Residuals:
#   Min      1Q  Median      3Q     Max 
# -4.9814 -2.1185  0.2217  1.0717  7.5186 
# 
# Coefficients:
#   Estimate Std. Error t value Pr(>|t|)    
# (Intercept)  37.8846     2.0738   18.27  < 2e-16 ***
#   mtcars$cyl   -2.8758     0.3224   -8.92 6.11e-10 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Residual standard error: 3.206 on 30 degrees of freedom
# Multiple R-squared:  0.7262, Adjusted R-squared:  0.7171 
# F-statistic: 79.56 on 1 and 30 DF,  p-value: 6.113e-10
# 画图
plot(mtcars$cyl,mtcars$mpg)
abline(lmfit)

稍微有点丑的图就横空出世了。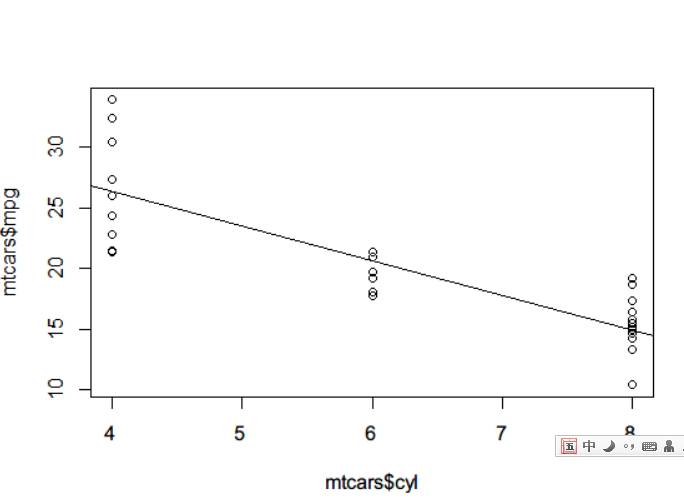F统计可以产生一个F统计量，是模型的均方和均方误差的比值。因此，当F统计量很大时，意味着原假设被拒绝，回归模型有预测能力。

3.7 执行二项分布检验

证明假设不是偶然成立的，而是具有统计显著性。

二项分布检验

library(stats)
binom.test(x=92,n=315,p=1/6)
 Exact binomial test

data:  92 and 315
number of successes = 92, number of trials = 315, p-value = 3.458e-08
alternative hypothesis: true probability of success is not equal to 0.1666667
95 percent confidence interval:
 0.2424273 0.3456598
sample estimates:
probability of success 
             0.2920635 

3.8 执行t检验

boxplot(mtcars$mpg, mtcars$mpg[mtcars$am==0], ylab="mpg", name=c("overall", "automobile"))
abline(h=mean(mtcars$mpg), lwd=2, col="red")
abline(h=mean(mtcars$mpg[mtcars$am==0]), lwd=2, col="blue")
t.test(mtcars$mpg~mtcars$am)
#########################
 Welch Two Sample t-test

data:  mtcars$mpg by mtcars$am
t = -3.7671, df = 18.332, p-value = 0.001374
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -11.280194  -3.209684
sample estimates:
mean in group 0 mean in group 1 
       17.14737        24.39231 

3.9 kolmogorov-smirnov检验

单样本检验用于比较样本是否符合某个已知序列（连续概率分布的相似性），双样本检验用于两个数据集累积分布方面的比较。

# 单样本
x <- rnorm(50)
ks.test(x,'pnorm')
###################
 One-sample Kolmogorov-Smirnov test

data:  x
D = 0.09625, p-value = 0.707
alternative hypothesis: two-sided
# 双样本，经验分布函数，ecdf
set.seed(3)
x<- runif(n=20, min=0,max=20)
y<- runif(n=20, min=0,max=20)
par(new=TRUE)
plot(ecdf(x), do.points=FALSE, verticals = T, xlim=c(0,20))
lines(ecdf(y), do.points=FALSE, verticals = T, lty=3)
ks.test(x,y)
##############
 Two-sample Kolmogorov-Smirnov test

data:  x and y
D = 0.3, p-value = 0.3356
alternative hypothesis: two-sided

两个p值均大于0.05，原假设成立。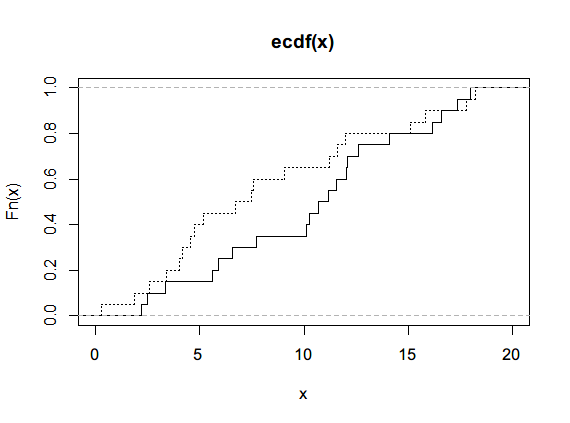

3.10 Wilcoxon秩和检验和Wilcoxon符号秩检验

非参检验，不需要假设样本服从正态分布

> wilcox.test(mtcars$mpg~mtcars$am,data=mtcars)

 Wilcoxon rank sum test with continuity correction
#############
data:  mtcars$mpg by mtcars$am
W = 42, p-value = 0.001871
alternative hypothesis: true location shift is not equal to 0

Warning message:
In wilcox.test.default(x = c(21.4, 18.7, 18.1, 14.3, 24.4, 22.8,  :
  无法精確計算带连结的p值

打结提示是因为有重复值，p值小于0.05，原假设不成立，自动和手动档汽车的mpg分布是不同的。

3.11 皮尔森卡方检验

> ftable <- table(mtcars$am, mtcars$gear)
> ftable
   ##############
     3  4  5
  0 15  4  0
  1  0  8  5
mosaicplot(ftable, main="手动和自动档前驱齿轮的马赛克图示意", color=TRUE)

皮尔森检验，必须保证输入样本满足下面两个条件：首先，输入数据集必须都是类别数据；其次，变量必须包含两个或以上独立数据组。

R还为用户提供了其他假设检验的方法：

  • 1.百分比检验prop.test: 用于测试不同样本集的百分比分布是否一致。
  • 2.Z检验（UsingT包中的simple.z.test）：比较样本均值与整体数据集均值以及标准偏差。
  • 3.Bartlett检验（Bartlett.test）：测试不同数据集的方差是否一致
  • 4.Kruskal-Wallis秩和检验（kruskal.test）：不确定数据集是否服从正态分布前提下，判断数据集的分布是否一致。
  • 5.Shapiro-Wilk检验（shapiro.test）：用于正态性检验。

3.12 单因素方差分析

方差分析，ANOVA（Analysis of Variance）,找到类别独立变量和连续非独立变量之间的关联，主要检验均值是否相同。仅包含一个类别变量作为独立变量，单因素方差分析。否则，包含两个或以上类别变量，要双因素方差分析。

# 首先，可视化
boxplot(mtcars$mpg~factor(mtcars$gear),xlab = 'gear', y='mpg')
# 然后，单因素方差分析
oneway.test(mtcars$mpg~factor(mtcars$gear))
###################该方法的优势是应用了Welch修正处理变量的不均匀性
 One-way analysis of means (not assuming equal variances)

data:  mtcars$mpg and factor(mtcars$gear)
F = 11.285, num df = 2.0000, denom df = 9.5083, p-value = 0.003085
# aov也可以，返回结果更非富
summary(aov(mtcars$mpg~as.factor(mtcars$gear)))
##################
                       Df Sum Sq Mean Sq F value   Pr(>F)    
as.factor(mtcars$gear)  2  483.2  241.62    10.9 0.000295 ***
Residuals              29  642.8   22.17                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# aov函数生成的模型也可以以表的形式输入摘要
model.tables(aov(mtcars$mpg~as.factor(mtcars$gear)))
# ############
Tables of effects

 as.factor(mtcars$gear) 
         3      4     5
    -3.984  4.443 1.289
rep 15.000 12.000 5.000
# TukeyHSD事后比较检验（多重比较检验）
TukeyHSD(aov(mtcars$mpg~as.factor(mtcars$gear)))
# ##############
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = mtcars$mpg ~ as.factor(mtcars$gear))

$`as.factor(mtcars$gear)`
         diff        lwr       upr     p adj
4-3  8.426667  3.9234704 12.929863 0.0002088
5-3  5.273333 -0.7309284 11.277595 0.0937176
5-4 -3.153333 -9.3423846  3.035718 0.4295874

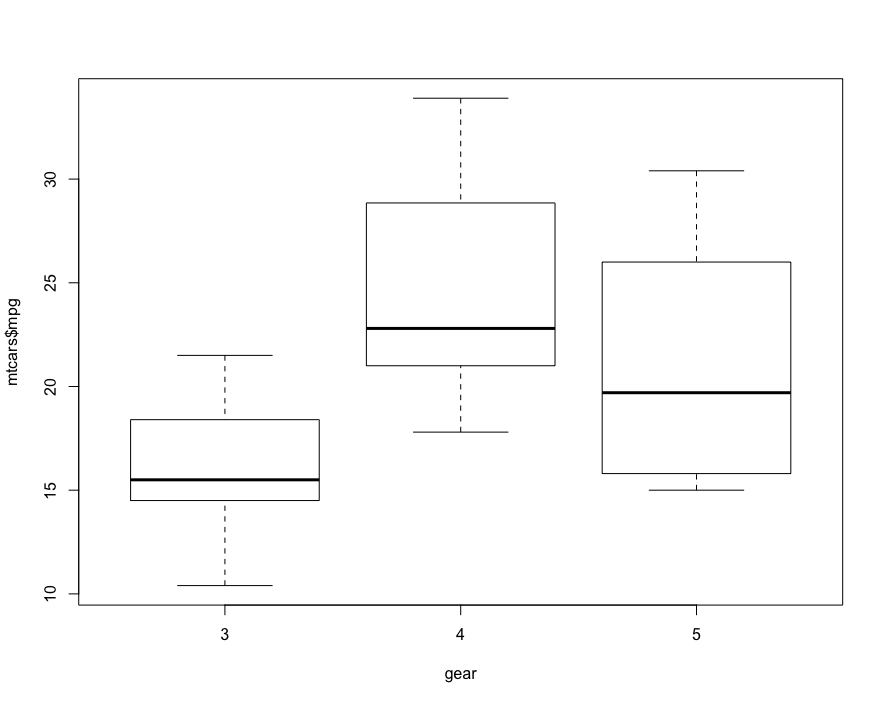F-score作为组间方差和组内方差的比值，如果整体F检验显著性水平较大，可以进一步事后检验，最常用的是Scheffe、Tukey-Kramer方法和Bonferroni修正。

3.13双因素方差分析

# 同样先可视化
par(mfrow=c(1,2))
boxplot(mtcars$mpg~mtcars$gear, subset = (mtcars$am==0), xlab = 'gear', ylab = 'mpg', main='automatic')
boxplot(mtcars$mpg~mtcars$gear, subset = (mtcars$am==1), xlab = 'gear', ylab = 'mpg', main='manual')
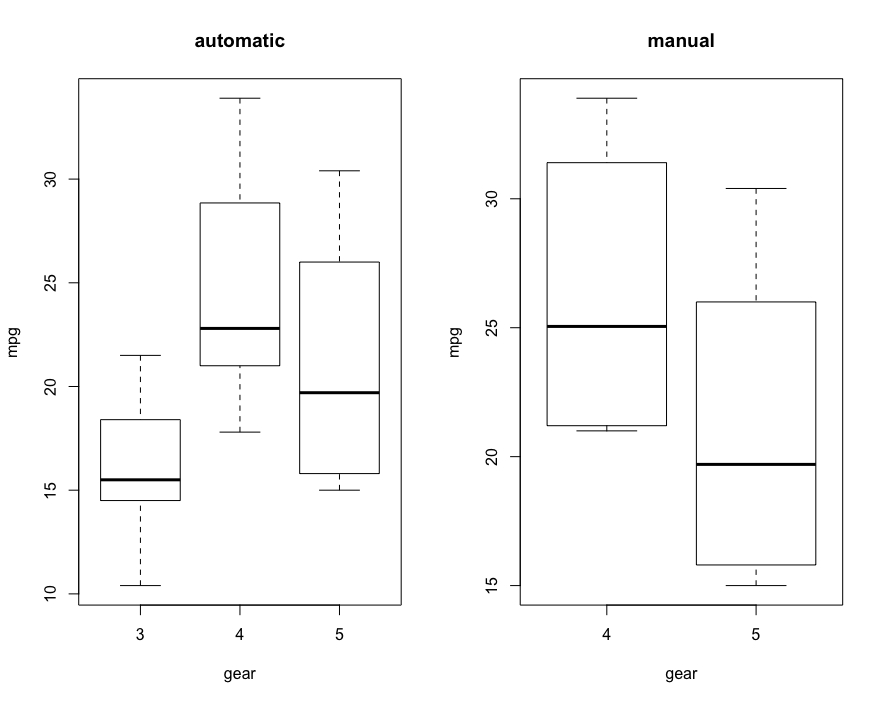
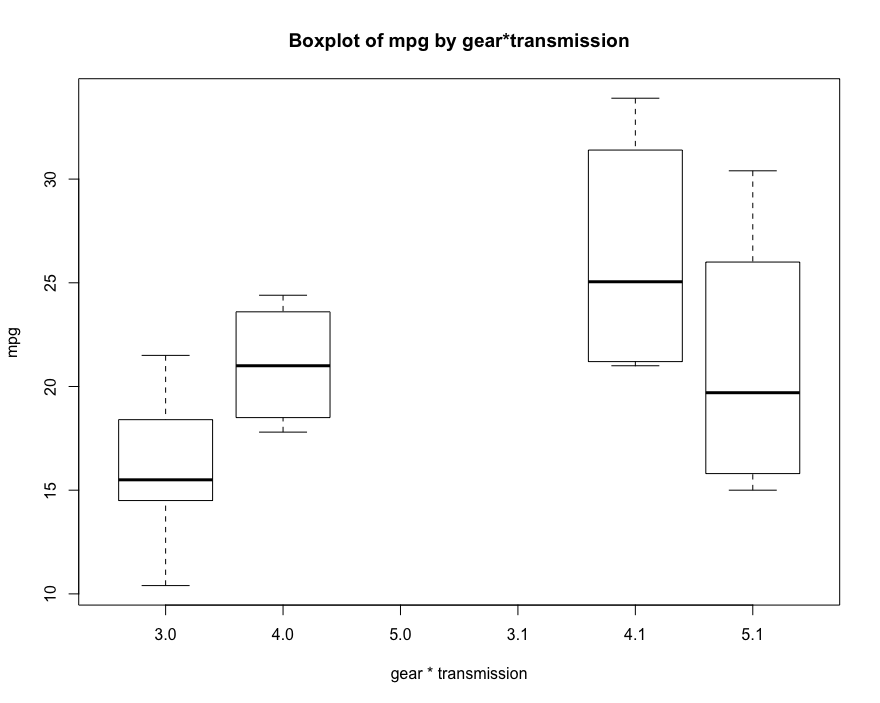
# 前驱齿轮*变速方式与mpg关联分析的盒图
boxplot(mtcars$mpg~factor(mtcars$gear)*factor(mtcars$am), xlab = 'gear * transmission', ylab = 'mpg', main='Boxplot of mpg by gear*transmission')
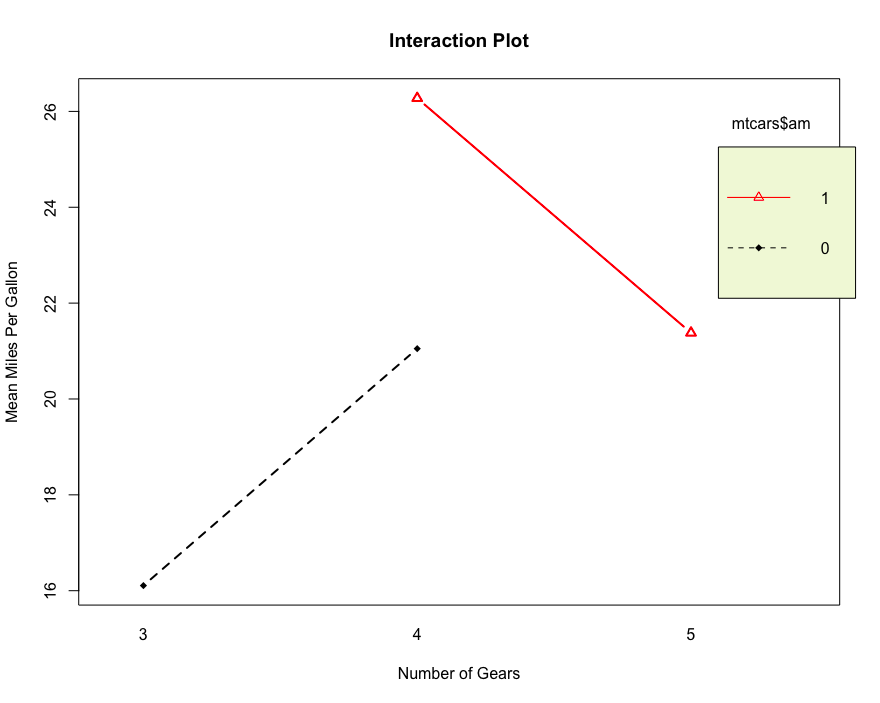
# 交互图来表达变量之间的关联
interaction.plot(mtcars$gear, mtcars$am, mtcars$mpg, type = 'b',col = c(1:3), leg.bty = 'o',leg.bg = 'beige',lwd=2, pch = c(18,24,22),
                 main = "Interaction Plot")
 # 双因素方差分析
summary(aov(mtcars$mpg~factor(mtcars$gear)*factor(mtcars$am)))
# #################
                    Df Sum Sq Mean Sq F value   Pr(>F)    
factor(mtcars$gear)  2  483.2  241.62  11.869 0.000185 ***
factor(mtcars$am)    1   72.8   72.80   3.576 0.069001 .  
Residuals           28  570.0   20.36                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 事后比较检验
TukeyHSD(aov(mtcars$mpg~factor(mtcars$gear)*factor(mtcars$am)))
# ###############
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = mtcars$mpg ~ factor(mtcars$gear) * factor(mtcars$am))

$`factor(mtcars$gear)`
         diff        lwr       upr     p adj
4-3  8.426667  4.1028616 12.750472 0.0001301
5-3  5.273333 -0.4917401 11.038407 0.0779791
5-4 -3.153333 -9.0958350  2.789168 0.3999532

$`factor(mtcars$am)`
        diff       lwr     upr     p adj
1-0 1.805128 -1.521483 5.13174 0.2757926
par(mfrow=c(1,2))
plot(TukeyHSD(aov(mtcars$mpg~factor(mtcars$gear)*factor(mtcars$am))))

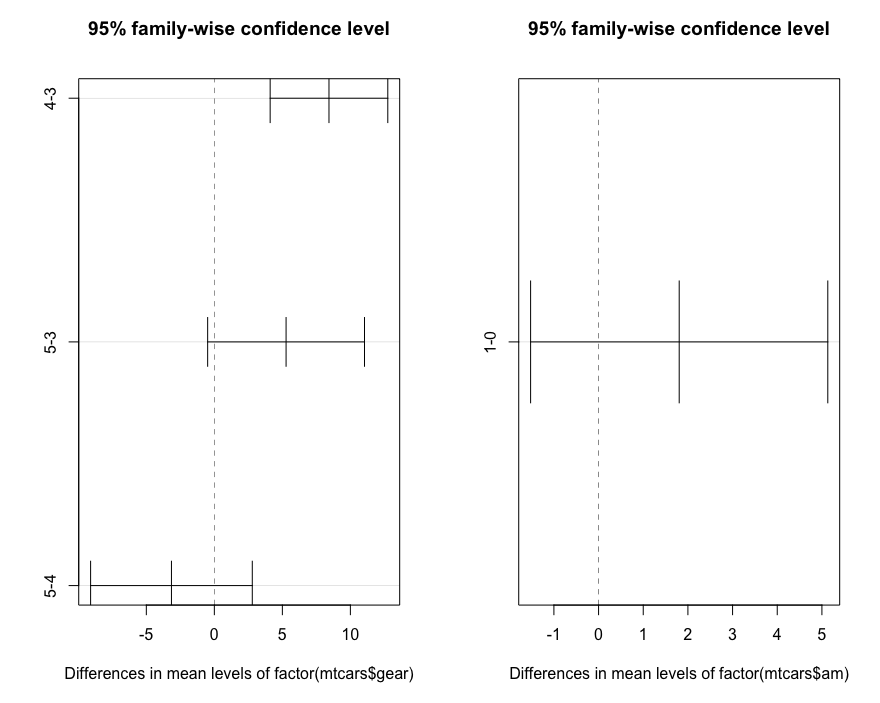扩展函数manova适用于多元变量分析，用于检验多元独立变量对多元非独立变量的影响。




欢迎微信交流






小编微信






扫描二维码

获取更多精彩

公众号





本篇文章来源于微信公众号: 微因

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注